MD5 的碰撞率
MD5 是一种经典的信息摘要算法,由 32 个 十六进制(2^4)的数字构成,共 128 位。类比概率问题:
- 从 10 个不同的球中有放回的任意取两次,各个球俩俩互不相同的概率为 P = 1 * 9/10,则发生碰撞的概率为 1 - P = 1/10
- 从 10 个不同的球中有放回的任意取三次,各个球俩俩互不相同的概率为 P = 1 * 9/10 * 8/10,则发生碰撞的概率为 1 - P = 28/100
- ……
- 从 N 个不同的球中有放回的任意取 n 次(n<=N),各个球俩俩互不相同的概率为 P = 1 * (N-1)/N * (N-2)/N * …… * (N-n+1)/N,则发生碰撞的概率为 1 - P
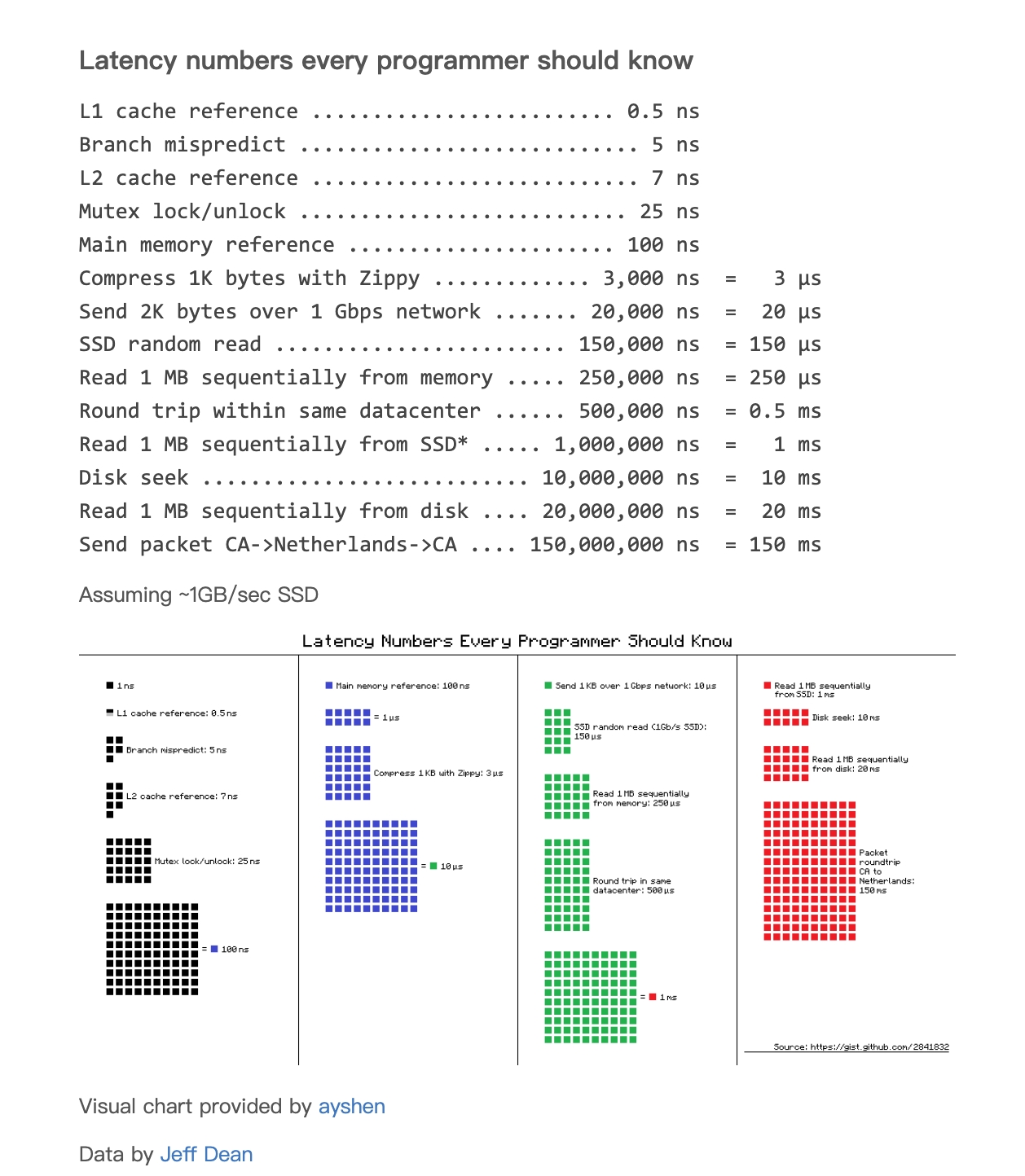
在固定容量下,随着取球的次数增多,发生碰撞的概率也会增加,Hash 碰撞问题与 Birthday Problem 非常类似,根据生日悖论,在 N = 365 天中要出现两个生日相同的人,所需人数为 n~O(√N) 量级,则 M 位长度的哈希表可能发生碰撞测试次数为 2^(M/2),得出 MD5 的意外碰撞率应该是 2^-64,即,在不故意创建冲突的情况下,平均需要对 2^64 个值进行 Hash 处理才能使它们之间发生单个冲突。目前集群统计出的文件数量约 170 亿(2^32 约等于 43 亿),远小于 2^64。下表展示了不同位数的哈希值,如果想要达到某个碰撞概率,需要尝试多少次。SATA 硬盘一个 bit 位出现数据错误的概率在 10^-18 到 10^-15 之间。作为比较,将哈希碰撞的概率控制在 10^-15 范围内已经相对来说非常安全了。
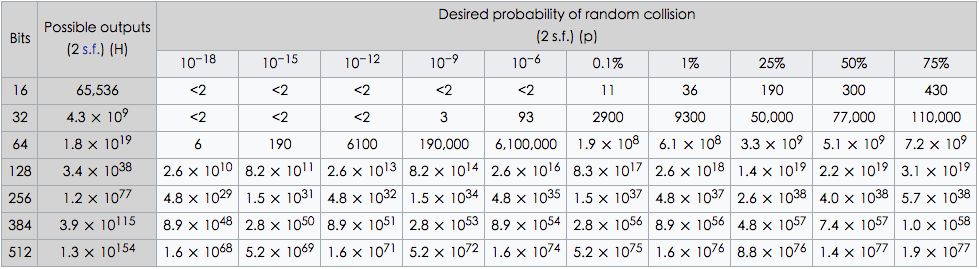
以第一行为例子,16bit 一共有 65536 个桶,要想平均发生碰撞的概率为 0.1%,只需要执行 11 次哈希,<2 说明无法达到这么低的概率
延伸阅读
延迟时间