概念
首先频繁项集挖掘和关联关系分析和聚类算法一样属于无监督学习。
本章节主要讲解下面会用到的一些重要概念与名词解释,先熟悉一下有助于理解算法过程。
频繁模式:模式可分为项集、子序列。假设数据库中有100条交易记录,其中80条交易记录中都包含牛奶和面包。牛奶和面包的组合就称为项集,频繁出现在数据库记录中的项集,就称为频繁项集。而如果项集是有先后顺序的,如先购买 PC 再购买键盘,那么 PC 和键盘的组合就称为子序列,同理频繁出现在数据库中的子序列就是频繁子序列。频繁项集和频繁子序列统称为频繁模式。
关联规则:在项集A={面包,牛奶}中,买面包的人也会买牛奶就是一对关联关系,关联关系表示为面包=>牛奶[support=60%,confidence=80%]。其中support是支持度,confidence是置信度。
支持度:在所有交易记录中,同时包含面包和牛奶的交易记录占交易记录总数的百分比,即 \(P( 面包 \cup 牛奶 ) \) 。
置信度:在所有交易记录中,包含面包的情况下包含牛奶的概率,即 \( P( 牛奶 | 面包 ) = \frac{ P( 面包 \cup 牛奶 ) }{ P( 面包 ) } \)
最小支持度阈值:支持度超过最小支持度阈值的项集称为频繁项集。
最小置信度阈值:满足最小支持度和最小置信度的关联规则成为强关联规则。
对于频繁项集挖掘,如果最小支持度计数设置的过小的话,会导致频繁项集过多,导致计算机无法处理。因为一个频繁项集的子集肯定也是频繁项集。一个长度为100的频繁项集,就会产生\(C_{100}^{1}\)个频繁一项集,\(C_{100}^{2}\)个频繁二项集… \(C_{100}^{1} + C_{100}^{2} + … + C_{100}^{100} = 2^{100}-1 \approx 1.27 * 10^{30} \)个频繁子项集。因此提出了闭频繁项集和极大频繁项集的概念。
闭频繁项集:对于项集X和项集Y,如果X是Y的真子集,不存在真超项集Y和项集X的支持度计数相等。那么称项集X是闭的,如果项集X是频繁项集,则X称为闭频繁项集。
极大频繁项集:对于频繁项集X,X是Y的子集,不存在超项集Y是频繁项集,那么项集X称为极大频繁项集。
Apriori
先验算法是发现频繁项集的最基本的算法,它通过限制候选产生发现频繁项集。
算法思想
先找出数据库中的所有频繁一项集L1,然后通过L1找出频繁二项集L2,以此类推,直到无法找到频繁k项集。
先验性质
先验性质:频繁项集的所有非空子集也一定是频繁的。对于一个非频繁项集I,添加项A到这个项集中,结果集\(I \cup A\)不可能比I更频繁,因此结果集也一定是非频繁的。
算法过程
找出每一个Lk就需要对数据库进行一次完整的扫描,但是基于先验性质可以压缩搜索空间。为了找出Lk,首先将Lk-1与自身连接产生候选k项集的集合。为了有效实现,Apriori算法默假定项集中的项是按字典顺序排好序的。这样,如果两个项集中的前k-2项是相同的,其他不同,则这两个项集是可连接的。例如,为了找出L4,项集{I1,I2,I3}和项集{I1,I2,I4}连接,产生的候选项集就是{I1,I2,I3,I4}。得到的候选项集不一定是频繁的,因此还需要扫描数据库,统计候选项集的支持度计数,确定是否是频繁项集,如果不是就从候选项集集合中剔除。
FP-growth
Apriori算法的局限性
Apriori算法尽管压缩了候选项集的规模,但是仍然可能受两种开销影响。
- 如果有10000个频繁一项集,就会产生\( C_{10000}^{2} \)个候选二项集
- 可能需要重复扫描整个数据库,去匹配检查一个很大的候选集计算每个候选项集的支持度。
Frequent-Pattern Growth
可以设计一种方法,挖掘全部频繁项集而无须这种昂贵的候选产生过程。这种方法就是频繁模式增长(Frequent-Pattern Growth)。它采取分治策略,将代表频繁项集的数据库压缩到一棵频繁模式树。该算法只需要扫描两次数据库就可以了。
例如某数据库中有如下交易记录:
| 交易记录ID | 购买列表 |
|---|---|
| T1 | I1,I2,I5 |
| T2 | I2,I4 |
| T3 | I2,I3 |
| T4 | I1,I2,I4 |
| T5 | I1,I3 |
| T6 | I2,I3 |
| T7 | I1,I3 |
| T8 | I1,I2,I3,I5 |
| T9 | I1,I2,I3 |
数据库第一次扫描和Apriori算法相同,首先得到频繁一项集,并记录频繁项集的支持度计数,按项集的支持度计数从大到小排序。例如:设最小支持度计数为2,有L1=({I2:7},{I1:6},{I3:6},{I4:2},{I5:2})。
然后开始构造FP树。首先创建树的根节点,初始化为null。开始第二次扫描数据库,将每条交易记录中的项都按L1中各项的次序从大到小排序,对于T1{I1,I2,I5}排序后就变成了{I2,I1,I5}。这就是FP-growth树的第一个分支。
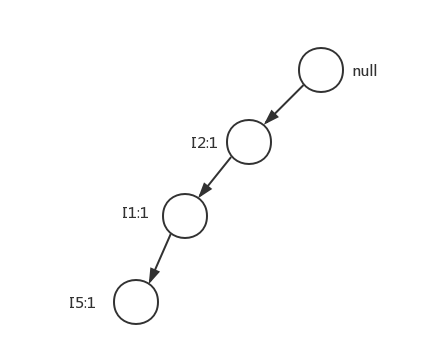
对于T2{I2,I4},排序后依然是{I2,I4}。又添加一个分支,因为I2子节点已经存在了,因此合并。
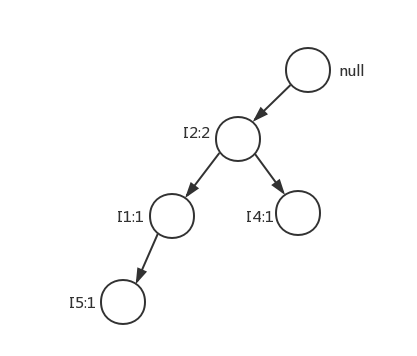
依次将各条排好序的交易记录添加到FP-growth树中。
| 交易记录ID | 购买列表 | 排序后 |
|---|---|---|
| T1 | I1,I2,I5 | I2,I1,I5 |
| T2 | I2,I4 | I2,I4 |
| T3 | I2,I3 | I2,I3 |
| T4 | I1,I2,I4 | I2,I1,I4 |
| T5 | I1,I3 | I1,I3 |
| T6 | I2,I3 | I2,I3 |
| T7 | I1,I3 | I1,I3 |
| T8 | I1,I2,I3,I5 | I2,I1,I3,I5 |
| T9 | I1,I2,I3 | I2,I1,I3 |
最终生成的FP-growth树如下:
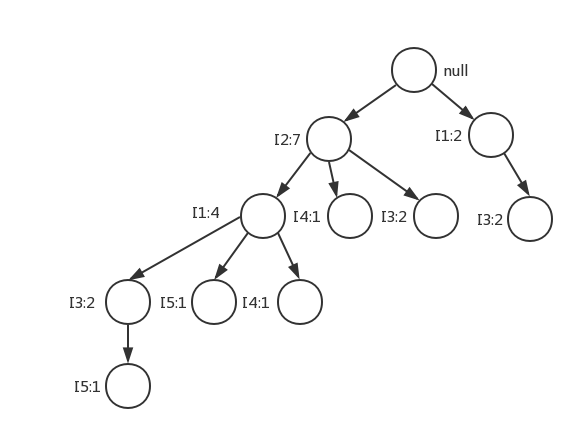
这样问题就由数据库频繁模式挖掘变成了FP树挖掘。挖掘FP树的过程如下:
- 首先从FP树中获得条件模式基
- 通过条件模式基,构建条件FP树
- 重复步骤1、2,直到构建完所有条件FP树。
从L1取出所有单个频繁项,按照L1倒序的顺序,分别构造条件模式基,条件模式基就是该节点的前缀路径上的节点组成的集合。例如I5的条件模式基就是({I2,I1,I3:1},{I2,I1:1})。然后将I5的条件模式基当作一个子数据库,构造I5的条件FP树。
首先计算I5的条件模式基构成的子数据库的L1(频繁一项集),为{I2:2,I1:2},得到后缀模式为I5的FP条件树如下。
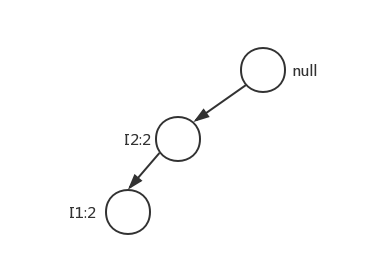
通过将条件模式树产生的所有频繁模式(频繁k项集)({I2:2}、{I1:2}、{I2:I1:2})与后缀模式{I5}分别进行连接进行模式增长,得到频繁模式{I2,I5:2}、{I1,I5:2}、{I2,I1,I5:2}。
L1中各项条件FP树挖掘如下表所示:
| 后缀模式 | 条件模式基 | 条件FP树 | 条件FP的频繁模式 | 模式增长 |
|---|---|---|---|---|
| I5 | {I2,I1:1}、{I2,I1,I3:1} | (I2:2,I1:2) | {I2:2}、{I1:2}、{I2,I1:2} | {I2,I5:2}、{I1,I5:2}、{I2,I1,I5:2} |
| I4 | {I2,I1:1}、{I2:1} | (I2:2) | {I2:2} | {I2,I4:2} |
| I3 | {I2,I1:2}、{I2:2}、{I1:2} | (I2:4,I1:2)、(I1:2) | {I2:4}、{I1:4}、{I2,I1:2} | {I2,I3:4}、{I1,I3:4}、{I2,I1,I3:2} |
| I1 | {I2:4} | (I2:4) | {I2:4} | {I2,I1:4} |
| I2 | 无 | 无 | 无 | 无 |
通过模式增长得到了所有频繁k项集(k>=2),至此就得到了所有交易记录的频繁模式。FP-growth将发现长频繁项集(长度>=2)的问题转换成了在较小的子数据库中递归搜索较短频繁模式,然后连接后缀模式,得到长频繁模式。该方法显著降低了搜索开销。
FP-Growth Python3.6 实现
# -*- coding: utf-8 -*-
class TreeNode:
""" FP 树 """
def __init__(self, name_value, num_occur, parent_node):
self.name = name_value
self.count = num_occur
self.parent = parent_node
# {itemName:treeNode}
self.children = {}
# 用于指向相同元素项所在的树节点
self.node_link = None
def __cmp__(self, other):
pass
def inc(self, num_occur):
self.count += num_occur
def display(self, index=1):
print('---' * index, '|', self.name, ':', self.count)
for child in self.children.values():
child.display(index + 1)
class FPGrowth:
def __init__(self, data_set, min_sup=1):
self.data_set = data_set
self.min_sup = min_sup
def __update_header(self, head_node, target_node):
"""
更新链表
:param head_node: 链表表头节点
:param target_node: 需要添加到链表尾部的节点
:return:
"""
while head_node.node_link is not None:
head_node = head_node.node_link
head_node.node_link = target_node
def __update_tree(self, items, in_tree, header_table, count):
"""
将一条排好序的记录链接到FP树的根节点
:param items: 排好序的一条记录
:param in_tree: 要更新的树节点
:param header_table: 项表头
:param count: 记录数
:return:
"""
# 若第一项是否已经存在,则更新树节点
if items[0] in in_tree.children:
in_tree.children[items[0]].inc(count)
else:
# 新添加的树节点
in_tree.children[items[0]] = TreeNode(items[0], count, in_tree)
if header_table[items[0]][1] is None:
# 该项第一次被添加到树中,记录该项元素的链表表头,TreeNode
header_table[items[0]][1] = in_tree.children[items[0]]
else:
# 将该节点添加到链表尾部
self.__update_header(header_table[items[0]][1], in_tree.children[items[0]])
if len(items) > 1:
# 对该条记录剩下的元素项递归调用update_tree
self.__update_tree(items[1::], in_tree.children[items[0]], header_table, count)
def __create_fp_tree(self, data_set, min_sup):
"""
构建FP树
:return:
"""
# 用字典来保存头指针表,除了存放指针外,还用来保存FP树中每类元素的总数
# {item:3}
header_table = {}
''' 第一次遍历数据集 '''
# 统计各项的支持度计数
for trans in data_set:
for item in trans:
header_table[item] = header_table.get(item, 0) + data_set[trans]
# 删除不满足最小支持度阈值的项,遍历keys的时候,python3会出现错误:
# dictionary changed size during iteration
# 转换成 list 就可以了
for item in list(header_table.keys()):
if header_table[item] < min_sup:
del header_table[item]
# 频繁一项集
freq_item_set = set(header_table.keys())
if len(freq_item_set) == 0:
return None, None
# {item:[3,None]}
for item in header_table:
# [项支持度计数,该项元素的链表表头]
header_table[item] = [header_table[item], None]
# 根节点
ret_tree = TreeNode('root', 1, None)
''' 第二次遍历数据集 '''
# frozenset, 1
for tran_set, count in data_set.items():
# 记录每一条记录各项元素的支持度,用于排序
local_data = {}
for item in tran_set:
if item in freq_item_set:
local_data[item] = header_table[item][0]
if len(local_data) > 0:
# 按各项的支持度计数从大到小排序 -> list [item]
ordered_items = [v[0] for v in sorted(local_data.items(), key=lambda p: p[1], reverse=True)]
self.__update_tree(ordered_items, ret_tree, header_table, count)
return ret_tree, header_table
def __ascend_tree(self, leaf_node, prefix_path):
"""
回溯所给节点的前缀路径
:param leaf_node:
:param prefix_path:
:return:
"""
if leaf_node.parent is not None:
prefix_path.append(leaf_node.name)
self.__ascend_tree(leaf_node.parent, prefix_path)
def __find_prefix_path(self, tree_node):
"""
找出所给项的所有条件模式基
:param tree_node:
:return:
"""
# 条件模式基
condition_patterns = {}
while tree_node is not None:
prefix_path = []
self.__ascend_tree(tree_node, prefix_path)
if len(prefix_path) > 1:
condition_patterns[frozenset(prefix_path[1:])] = tree_node.count
tree_node = tree_node.node_link
return condition_patterns
def __recursive_fp_tree(self, header_table, min_sup, prefix_path, freq_item_list):
"""
递归遍历FP树的所有条件FP树
:param header_table:
:param min_sup:
:param prefix_path:
:param freq_item_list:
:return:
"""
# 按各项支持度计数从小到大的顺序开始分别挖掘的条件FP树
find_freq_list = [v[0] for v in sorted(header_table.items(), key=lambda p: p[1][0])]
for item in find_freq_list:
new_freq_set = prefix_path.copy()
new_freq_set.add(item)
freq_item_list.append(new_freq_set)
condition_pattern = self.__find_prefix_path(header_table[item][1])
condition_fp_tree, new_head_table = self.__create_fp_tree(condition_pattern, min_sup)
if new_head_table is not None:
self.__recursive_fp_tree(new_head_table, min_sup, new_freq_set, freq_item_list)
def get_freq_items(self):
"""
获取频繁项集
:return: 频繁项集
"""
fp_tree, head_table = self.__create_fp_tree(self.data_set, self.min_sup)
freq_items_list = []
self.__recursive_fp_tree(head_table, 2, set([]), freq_items_list)
return freq_items_list
def load_data():
"""
加载数据
:return:
"""
ret_dict = {}
simple_data = [
['I1', 'I2', 'I5'],
['I2', 'I4'],
['I2', 'I3'],
['I1', 'I2', 'I4'],
['I1', 'I3'],
['I2', 'I3'],
['I1', 'I3'],
['I1', 'I2', 'I3', 'I5'],
['I1', 'I2', 'I3']
]
for trans in simple_data:
# frozenset 是不可变的 set 集合
# 可以直接将其作为字典的 key,也可以作为其他集合的元素。
# 没有 add 和 remove 方法
ret_dict[frozenset(trans)] = 1
return ret_dict
if __name__ == '__main__':
data = load_data()
print(FPGrowth(data, 2).get_freq_items())
由频繁项集产生关联规则
发现频繁项集后,就可以通过频繁项集直接产生强关联规则。对于频繁项集T的每个非空子集S,如果support(T)/support(S)大于最小置信度阈值,则就产生强规则S=>(T-S)





