基本概念
分类是一种重要的数据分析形式,例如有一批教师家访的数据,要根据这些数据来将教师分成敬业的非敬业的两类,这个数据分析任务就叫做分类(classification)。
分类需要构造一个叫分类器(classifer)的模型来预测类标号,例如教师敬业是0,非敬业是1。像这种只有有限个分类结果的分类,分类结果可以用离散值来表示,且值之间的次序没有意义。
而如果你是要预测某顾客在某商场的一次购物要花多少钱,这种分析任务就属于数值预测(numeric prediction),它预测一个连续值或者有序值。这种模型就叫预测器(predictor)。回归分析(regression analysis)是数值预测中最常用的统计学方法。本篇主要讲解分类。
分类的一般过程
分类一般有两个阶段
- 学习阶段(构建分类器)
通过已知类标号的数据集进行分析训练,构造分类器,训练数据集中的每一条数据由N个属性和当前数据的所属类标号构成。类标号是离散的、无序的。因为提供了每条数据的所属类标号,因此属于监督学习(supervised learning)。此阶段可以看成构造一个映射函数y=f(X),X是数据集中的某一条数据,y是X所属的类标号。
- 分类阶段(用分类器预测给定数据的类标号)
如果使用训练集来度量分类器的准确率,结果可能是乐观的,因为分类器趋向于过拟合(overfit),它可能在学习期间包含了一些特殊的异常数据,而这些异常数据在实际中并不存在。因此应该用独立的于训练集的一组数据来进行准确率的检测。
决策树
为什么用决策树进行分类:
- 顾名思义,决策树是一种树结构,用树的方式表示分类条件是直观的,且容易被人理解。
- 决策树分类器的构造不需要任何领域的知识或参数设置,因此适合探索式知识发现。
- 决策树可以处理高维数据。
- 决策树的归纳学习和分类步骤是简单而又快速的,而且具有很好的准确率。
例如根据顾客信息预测顾客是否购买计算机的决策树如下图:
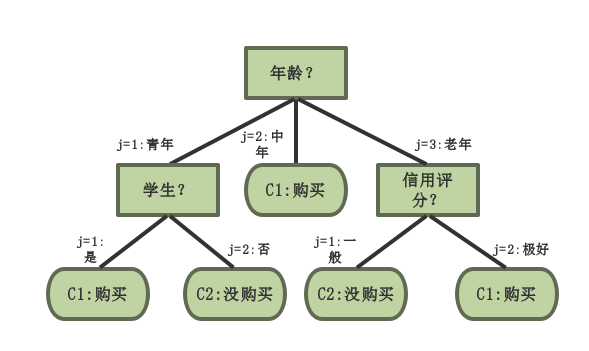
决策树归纳
现实中人通过主观意念来构造决策树,而机器是怎么构造决策树的呢?
决策树的主要算法包括ID3、C4.5、CART,它们采用贪心策略,以自顶向下递归的分治方法构造决策树。
算法的三个输入参数:D,attribute_list,attribute_selection_method
- D: 训练数据集,包含N条数据,每条数据由M个属性的值和所属的类标号构成。
- attribute_list: 候选属性的集合,初始是除所属类标号之外的所有属性,后续会随着算法的分支而减少。
- attribute_selection_method: 选择属性的度量方式,例如信息增益、基尼系数等。树是否会被构造成严格的二叉树取决于属性的度量方式,如基尼系数强制结果树是二叉树,而信息增益允许多路划分。
算法 generate_decision_tree(Dj, attribute_list),由数据集D中的训练数据产生决策树。 大致流程如下:
- 创建一个节点N;
- if \( D \) 中所有数据都属于同一类 \( C \) ,(例如上图中所有的中年都属于购买计算机的一类。)
- then 将节点N置为叶节点,并以类 \( C \) 标记,返回叶节点N
- if attribute_list.size == 0,即所有的属性都已经作为分裂属性用过了
- then 将节点N置为叶节点,以多数表决的方式,选取D中数据占比最大的类标号对节点进行标记,返回N
- else 使用attribute_selection_method(D, attribute_list)找出最好的分裂标准(能将D划分的更纯,划分出的每一个子类的绝大多数数据的所属类标号相同),并用分裂标准标记节点N
- if 分裂标准中的分裂属性A是离散的且允许多路划分
- then 将分裂属性A从attribute_list移除
- for 分裂标准中的每个输出 j (划分数据并对每个分区产生子树),设\( D_j \)是\( D \)中划分到 \( j \) 数据分区的数据集
- if \( D_j \) 为空,即当前分支没有数据
- then 加一个树叶到节点N,标记为D中的多数类
- else 加一个由 generate_decision_tree(Dj, attribute_list) 返回的节点到N
- endfor
- 返回结果决策树N
属性的度量方式
属性选择度量是一种分裂标准,选择哪个属性按什么标准进行划分能将数据分类分的更纯——即分完的类中的绝大多数数据都属于同一类标号。属性选择度量给所有的属性提供了秩评定,选取当前评分最高的属性(即将数据分的最纯的属性)作为当前的分裂属性。
常用的三种评分方式:
- 信息增益:
选择具有最高信息增益的属性作为节点N的分裂属性,该属性使结果分区中对数据分类所需要的信息量最小,并反映这些分区中的不纯性。此种方式使得对分区进行分类所需要的期望测试数目最小,并确保找到一个简单的(但不一定是最简单的)树。
对D中数据分类所需要的期望信息由下式给出: \[ Info(D) = - \sum_{i=1}^m p_i\log_2(p_i) \]
其中 \( p_i \) 是数据集D中的任意数据 \( x \) 属于类 \( C_i \) 的概率,\( p_i = | C_i | / | D | \),\( Info(D) \)是要识别D中数据的类标号所需要的平均信息量,又称为 \( D \) 的熵(entropy)。熵越大,数据 \( x \) 所属类的不确定性就越大。例如 \( p_1 = 0.5 \), \( p_2 = 0.5 \) 和 \( p_1 = 1.0 \), \( p_2 = 0.0 \),很明显第一种的熵更大。
现假设我们要按属性A将 \( D \) 中的数据进行划分,其中A属性根据训练数据的观测有 \( v \) 个不同值 \( { a_1,a_2,\ldots,a_v} \),如果A是离散的,那么这 \( v \) 个值将对应与属性A上测试的 \( v \) 个输出分区 \( {D_1,D_2,\ldots,D_v } \),对于 \( D_j \) 中的数据,他们的属性A都是 \( a_j \)。这些分区对应于从节点N生长出来的 \( v \) 个分支。我们希望此次划分能将每个分区都划分的更纯,但实际上多半是不纯的,例如 \( D_1 \) 中可能70%是 \( C_1 \) 类,30%是 \( C_2 \) 类。在此次划分之后,为了得到更准确的分类,我们还需要多少信息呢?这个量由下面的式子来描述: \[ Info_A(D) = \sum_{j=1}^v \frac{|D_j|}{|D|}*Info(D_j) \]
其中\( \frac{|D_j|}{|D|} \)是第\( j \)个分区的权重。\( Info_A(D) \)是对 \( D \) 按属性A进行数据分类后还需要的期望信息量,需要的期望信息越小,分区的纯度越高。
信息增益描述了本次划分后,我们得到了多少信息量,即原来的信息需求量减去划分后的信息需求量: \[ Gain(A) = Info(D) - Info_A(D) \]
所以,我们选择拥有最大信息增益的属性作为当前的分裂属性。对于一个数据集D,它的熵 \( Info(D) \) 是固定的,所以我们只需要计算最小的 \( Info_A(D) \),就可以选出当前的最佳分裂属性。
上面的例子是在属性A是离散的情况下,那么如果属性A的值是连续的值呢?在这种情况下,就需要确定A的最佳分裂点了,分裂点是A上的阈值。
首先,将A的值进行递增排序,典型的,每对相邻值的中点看作是可能的分裂点,这样如果 A 有 \( n \) 个值,那么就需要计算 \( n-1 \) 次分裂点。对A的每个可能的分裂点,计算其 \( Info_A(D) \),其中 \( v=2 \),共两个数据分区\( D_1 \)(\( A\leq split\_point \))、\( D_2 \)(\( A\geq split\_point \)),选择最小\( Info_A(D) \)的点作为分裂点。
- 增益率:
信息增益度量倾向于选择具有大量值的属性。例如,当某一属性productId是数据的唯一标识,当按此属性进行数据划分时,每个数据分区都只有一条数据,所以每个数据分区中的数据都是纯的,它属于某一类的概率都是1.0,所以 \( Info(D_j) \) = 0, 所以\( Info_{productId}(D) \) = 0。因此对该属性的划分得到的信息增益一定是最大的。然而这种划分对数据分类没有任何意义。
ID3的后继C4.5使用增益率(gain ratio)作为信息增益的扩充,试图克服这种偏倚。它用分裂信息将信息增益规范化。分裂信息的定义: \[ SplitInfo_A(D)= - \sum_{j=1}^v \frac{|D_j|}{|D|}*\log_2(\frac{|D_j|}{|D|}) \]
该值代表由训练数据集D划分成对应与属性A的 \( v \) 个输出的不确定性 ,它与熵\( Info(D) \)不同,熵考虑的是数据分类的不确定性。
增益率定义: \[ GainRate(A)=\frac{Gain(A)}{SplitInfo_A(D)} \]
选择最大增益率的属性作为分裂属性。然而分裂信息趋向于0时,改比率会变得不稳定。为了避免这种状况,增加一个约束:选取的测试的分裂信息增益必须要大,至少与考察的所有测试的平均增益一样大,这样就避免了分裂信息的值趋于0。
- 基尼系数:
基尼系数(Gini index)CART中使用,基尼系数度量数据分区或数组集D的不纯度,定义如下: \[ Gini(D)=1-\sum_{i=1}^m p_i^{2} \]
其中 \( p_i \) 和熵中的含义相同。
基尼系数考虑每个属性的二元划分。首先来看离散值属性的情况。假设属性A有 \( v \) 个不同值 \( { a_1,a_2,\ldots,a_v} \) 。为确定A上最好的二元划分,需要知道A所有可能值构成集合的所有子集,每个子集\( S_A \)可以看作是 \( A\in S_A? \) 的二元测试。A 存在 \( 2^v \) 个子集,去掉 \( { a_1,a_2,\ldots,a_v} \) 和 \( \phi \),基于A的二元划分,存在 \( \frac{2^v-2}{2} \) 种形成数据集D的两个分区的可能方法。
按A属性进行二元划分,计算每个结果分区的不纯度的加权和,有如下公式: \[ Gini_A(D) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2) \]
对于离散属性,选择该属性产生的最小基尼系数的子集作为它的分裂子集。而对于连续值属性,需要考虑每一个可能的分裂点,策略类似与信息增益,在此不再赘述。对离散或连续属性的二元划分导致的不纯度的降低为: \[ Gini(D)-Gini_A(D) \]
具有最大不纯度降低,或者最小基尼系数的属性作为分裂属性。该属性和它的分裂子集或分裂点一起构成分裂准则。





